Giải Toán 12 trang 63 tập 1 Cánh diều
Giải Toán 12 trang 63 Cánh diều Tập 1
Giải Toán 12 trang 63 Tập 1 hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Cánh diều tập 1 trang 63.
Bài 1 trang 63 SGK Toán 12 tập 1
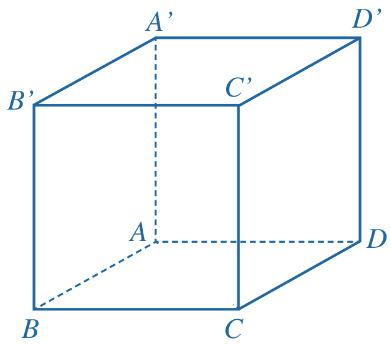
Cho hình hộp ABCD. A'B'C'D'. Vecto 
\(\vec{u}=\overrightarrow{A'A}+\overrightarrow{A'B'}+\overrightarrow{A'D'}\) bằng vectơ nào dưới đây?
A. \(\overrightarrow {A'C\;}\)
B. \(\overrightarrow {CA'}\)
C. \(\overrightarrow {AC'}\)
D. \(\overrightarrow {C'A}\)
Hướng dẫn giải:
Đáp án đúng: A
Áp dụng quy tắc hình hộp, ta có: \(\overrightarrow{A'A}+\overrightarrow{A'B'}+\overrightarrow{A'D'}=\overrightarrow{A'C}\)
Bài 2 trang 63 SGK Toán 12 tập 1
Cho tứ diện ABCD. Chứng minh rằng:
a) \(\overrightarrow{AC}+\overrightarrow{BD}=\overrightarrow{AD}+\overrightarrow{BC}\)
b) \(\overrightarrow{AB}-\overrightarrow{CD}=\overrightarrow{AC}+\overrightarrow{DB}\)
Hướng dẫn giải:
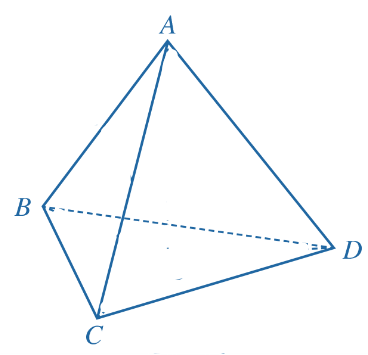
a) Ta có:
\(\overrightarrow{AC}+\overrightarrow{BD}=\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{BD}\)
\(=(\overrightarrow{AB}+\overrightarrow{BD})+\overrightarrow{BC}\)
\(=\overrightarrow{AD}+\overrightarrow{BC}\)
b) Ta có:
\(\overrightarrow{AB}-\overrightarrow{CD}=\overrightarrow{AC}+\overrightarrow{CB}-\overrightarrow{CD}\)
\(=\overrightarrow{AC}+(\overrightarrow{CB}-\overrightarrow{CD})\)
\(=\overrightarrow{AC}+\overrightarrow{DB}\)
Bài 3 trang 63 SGK Toán 12 tập 1
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Tính
a) \(\overrightarrow{A'B}.\overrightarrow{D'C};\overrightarrow{D'A}.\overrightarrow{BC}\)
b) Các góc \(( {\overrightarrow {A'D} ,\overrightarrow {B'C'} }); ( {\overrightarrow {AD',} \overrightarrow {BD} } )\)
Hướng dẫn giải:
Ta có: \(\overrightarrow{A'B}=\overrightarrow{D'C}\) nên \((\overrightarrow{A'B}=\overrightarrow{D'C})=(\overrightarrow{A'B}=\overrightarrow{A'B})= 0^{\circ}\)
Do đó \(\overrightarrow{A'B}.\overrightarrow{D'C}=\left|\overrightarrow{A'B}\right|.\left|\overrightarrow{D'C }\right|.\cos 0^{\circ}=a\sqrt{2} . a\sqrt{2}=2a^2\)
-----------------------------------------------
---> Xem thêm: Giải Toán 12 trang 64 tập 1 Cánh diều
Lời giải Toán 12 trang 63 Tập 1 Cánh diều với các câu hỏi nằm trong Toán 12 Cánh diều Bài 1: Vectơ và các phép toán vectơ trong không gian, được VnDoc biên soạn và đăng tải!
